Fizyka teoretyczna i biologia – na pierwszy rzut oka wydaje się, że te dwie dyscypliny naukowe mają ze sobą niewiele wspólnego. Tymczasem wiedza zarówno fizyczna, jak i matematyczna, może pomóc zrozumieć podstawy zjawisk ze świata natury. Potwierdzają to badania naukowe dr hab. Joanny Szymanowskiej-Pułki, prof. UŚ, która zajmuje się modelowaniem wzrostu roślin oraz bada własności mechaniczne tkanek roślinnych.

Dr hab. Joanna Szymanowska-Pułka, prof. UŚ

Ujarzmienie natury za pomocą języka matematyki sprawia, że naukowcy lepiej zrozumieją jej prawa. Musi być ono jednak podparte badaniami empirycznymi, które pozwalają weryfikować model. Przekonuje o tym prof. Joanna Szymanowska-Pułka, podkreślając, iż budowanie matematycznego modelu musi mieć swoje „korzenie” w samej naturze.

Naukowiec z Uniwersytetu Śląskiego w Katowicach łączy w swych badaniach zagadnienia z pogranicza biofizyki i morfogenezy roślin. Pracowała z nieżyjącym już prof. Zygmuntem Hejnowiczem, autorem definicji tensora wzrostu, oraz z jego uczniem prof. Jerzym Nakielskim, który opracował tensorowy model wzrostu organów roślinnych. Jest to niezwykle interesujące narzędzie pozwalające opisać rozwój układu komórek różnych organów roślinnych.

Jak wyjaśnia badaczka, sąsiadujące ze sobą komórki roślin są połączone ścianami w taki sposób, że nie przemieszczają się względem siebie. Rosną i dzielą się, zachowując jednak ten kontakt. Wzrost u roślin ma więc charakter ciągły, co umożliwia jego opis tensorowy. Z kolei podziały komórek przypominają, w dużym uproszczeniu, „wstawianie” nowych ścian. Reguły owego „wstawiania” zostały dosyć dobrze opisane, zaś atrybuty tensora wzrostu pozwalają na stosunkowo proste zastosowanie tych reguł w modelowaniu wzrostu organów roślinnych.

– Wszystkie organy roślinne rozwijają się w ten fascynujący sposób – skoordynowany i przez to cieszący oko matematyka. Zasady są dość proste. Wystarczy zapisać je językiem matematycznym – komentuje prof. Joanna Szymanowska-Pułka.

Naukowiec stosuje więc równania pozwalające wskazać położenie, w którym znajdzie się wybrany punkt danej komórki po upływie określonego czasu. Równania te opisują pole szybkości przemieszczeń poszczególnych punktów organu. Ogólna postać pola dla danego organu jest podobna dla różnych gatunków, ale by opisać konkretny przypadek, trzeba dobrać współczynniki określające granice stref organu i te decydujące o szybkości wzrostu.

Dopiero zastosowanie tensora wzrostu wraz z wyspecyfikowanymi współczynnikami umożliwia opisać sam wzrost, czyli nieodwracalną zmianę kształtu i układu komórek wybranego organu rośliny. Co ciekawe, najważniejszych danych dostarcza obserwacja empiryczna komórek pod mikroskopem.

– Ja przyglądam się przede wszystkim korzeniom bocznym, a dokładniej – obserwuję, jakie zmiany zachodzą w układzie komórek w czasie ich rozwoju u wybranych gatunków roślin. Chcę wiedzieć między innymi, jak się inicjują i rozwijają. Prowadząc badania, dążę do tego, aby poznać sekwencję zdarzeń podczas wzrostu – podkreśla biofizyk.

Korzenie boczne, które stanowią główny przedmiot zainteresowań badawczych prof. Joanny Szymanowskiej- -Pułki, pełnią dwie główne funkcje. Po pierwsze, zakotwiczają roślinę w podłożu, po drugie, zwiększają jej powierzchnię pobierającą substancje odżywcze z gleby. Im bardziej rozbudowany jest ten system, tym stabilniejsza i lepiej odżywiona będzie roślina. Prowadzone badania służące poznaniu procesu wzrostu korzeni mogą mieć więc istotne znaczenie chociażby dla rolnictwa. Roślina dobrze odżywiona daje bowiem lepsze plony, a stan korzeni wpływa na jej kondycję.

– Moje pierwsze badania dotyczyły rzodkiewki (Raphanus sativus), której poświęciłam rozprawę doktorską. Potem zajęłam się rzodkiewnikiem (Arabidopsis thaliana), rośliną bardziej przewidywalną w rozwoju, mającą prostszy układ komórek korzenia. To znacznie ułatwiło prowadzenie analiz – mówi badaczka.

Model wzrostu korzenia bocznego Arabidopsis thaliana

– Nie bez powodu rzodkiewnik jest w biologii rośliną modelową. Z jednej strony pięknie widać pod mikroskopem układ jego komórek, z drugiej – niewielka ich liczba sprawia, że scenariusze rozwoju korzenia bocznego są powtarzalne. Rzodkiewka okazała się bardziej skomplikowana pod tym względem – dodaje.

U obu gatunków występuje tak zwany palowy system korzeniowy, składający się z korzenia głównego oraz korzeni bocznych. W szczytowej części korzenia znajduje się wierzchołek, który ma kształt paraboloidy i składa się z korzenia właściwego i chroniącej go czapeczki. Wierzchołek zawiera komórki merystematyczne, czyli takie, które rosną i dzielą się. W szczytowej części korzenia właściwego umiejscowione jest centrum spoczynkowe otoczone przez szybko dzielące się komórki inicjalne, które dają początek wszystkim tkankom korzenia.

W tym miejscu warto wspomnieć o ciekawych właściwościach centrum spoczynkowego. Jak wyjaśnia naukowiec, tworzą je komórki rzadko dzielące się. Jeśli doszłoby do uszkodzenia części wierzchołka, wówczas komórki centrum spoczynkowego zaczęłyby się dzielić i mogłyby przejąć funkcje komórek inicjalnych – po to, aby odtworzyć uszkodzony wierzchołek i umożliwić dalsze funkcjonowanie pomimo mechanicznego defektu.

– Rośliny są świetnie przygotowane do życia. W ich rozwoju wszystko jest mistrzowsko zorganizowane i zaplanowane. Z przyjemnością poznawałam szczegóły dotyczące ich rozwoju, a dokładniej – wspomnianych przed chwilą korzeni bocznych – podkreśla naukowiec.

Z merystemu wierzchołka korzenia powstaje cała podziemna część rośliny. Warto jednak wiedzieć, że zarówno wierzchołek pędu, jak i korzenia, wykształcane są już w życiu embrionalnym rośliny. Korzenie boczne powstają natomiast postembrionalnie. Mają one pochodzenie endogenne, co oznacza, że są inicjowane wewnątrz korzenia macierzystego. To jeden z kluczowych czynników wpływających na ich rozwój.

Aby opracować symulację komputerową tego wzrostu, prof. Joanna Szymanowska-Pułka prowadziła obserwacje mikroskopowe korzeni bocznych u Arabidopsis thaliana.

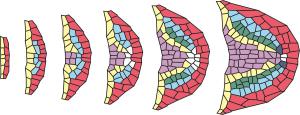
– Jeśli przekroimy korzeń główny Arabidopsis poprzecznie, możemy dostrzec różne tkanki – najbardziej wewnętrzne waskularne, następnie jednowarstwowe: perycykl, endodermę, korę i epidermę. Zawiązki korzeni bocznych pojawiają się w perycyklu zbudowanym z wąskich, dosyć długich komórek. Przy inicjowaniu sąsiednie komórki dzielą się nierówno, a następnie rozrastają się na szerokość. W dalszych etapach następują ich podziały poprzeczne i podłużne, co dobrze widać na dołączonej powyżej sekwencji, która jest efektem modelowania wzrostu tego organu. Widoczne na pierwszym obrazku dwie warstwy powstały w wyniku podłużnego przekroju komórek perycyklu, z nich powstają kolejne komórki. Przy czym nie dzielą się równomiernie, a w taki sposób, że możemy zaobserwować charakterystyczne dla zawiązków uwypuklenie. Kolory odnoszą się tu do różnych tkanek, a ich wykształcanie w modelu odzwierciedla rzeczywisty przebieg formowania się pratkanek w zawiązku korzenia bocznego – wyjaśnia naukowiec.

Temat wydaje się szczególnie interesujący z perspektywy biofizyka, chociażby ze względu na towarzyszące temu procesowi oddziaływania mechaniczne. Korzeń boczny musi się bowiem przebić przez pokrywające go warstwy komórek korzenia macierzystego, a to ma duże znaczenie dla rozwoju całego układu.

– Gdy opracowałam taki model dla korzenia bocznego rzodkiewki i nałożyłam go na obraz rzeczywistego korzenia, uzyskałam praktycznie identyczny kształt i układ komórek. To potwierdziło wiarygodność modelu. Dzięki temu można się więcej dowiedzieć o samej naturze – mówi badaczka.

Jak dodaje, opracowując ów model, posługuje się językiem matematyki i podgląda, w jaki sposób natura radzi sobie z takimi zagadnieniami, jak podziały komórek. Przetłumaczenie jej języka na język matematyki sprawia, że lepiej ją rozumiemy, poznajemy jej prawa.

Prof. Joanna Szymanowska-Pułka obecnie zajmuje się również badaniem układu komórek korzeni bocznych u mutantów Arabidopsis z defektami wzrostu korzenia oraz ze zmienionym składem ściany komórkowej. Chce sprawdzić, czy skład ściany może wpływać na kształt zawiązka korzenia bocznego. Wiele wskazuje na to, że im sztywniejsza ściana komórkowa, tym bardziej zdeformowane są zawiązki korzeni bocznych, bo podlegają większemu mechanicznemu naciskowi pokrywających je warstw komórek korzenia macierzystego. Takie przypadki także można opisać przy użyciu języka matematyki.

– Chcemy sprawdzić, jakiego typu są to defekty. Nasze analizy pozwoliły już stwierdzić, że jest zaledwie kilka grup takich zmian w morfologii, nie mają one charakteru dowolnego. Zamierzam znaleźć odpowiedź właśnie w oddziaływaniach mechanicznych – podsumowuje biofizyk.